Minority Games (past research on complex systems)
The minority game is a simple, yet realistic model of an evolving population in which individual agents compete for limited resources, without direct interaction between them. In its evolutionary version, agents adapt their behavior according to their past experience. Such systems can be found in various sciences such as social, biological and economical sciences. At each turn of this game agents choose between two options (like buying or selling in a stock market) where the only knowledge they have about the system is which one of the choices (e.g. buying or selling) was more beneficial so far (the ‘preferred choice’). At the end of each turn, agents belonging to the smaller group (the minority) are the winners; each of them gains points (a `prize'; e.g., a broker that sells when everybody else is buying earns money), while agents belonging to the majority lose points (a `fine'; e.g., a broker that buys when everybody else is buying loses money). Each agent has her own decision-making strategy, which is the probability that she will make the ‘preferred choice’. The agents change their strategies according to their success in the past.
As a side project during my Ph.D studies I wrote, together with a fellow Ph.D student, a paradigm shifting paper on minority games. The common wisdom at that time was that the best game strategy is to be consistent (either always taking the ‘preferred choice’ or always taking the other choice). We have shown that this conclusion is not a general property of the minority game, but depends on the prize to fine ratio. If agents gain for a right decision the same as they lose for a wrong one then consistency is beneficial. However, if the fine is larger than the prize then the best strategy is to be indecisive (i.e., to toss a coin at each turn). Later, in a following set of papers we have shown that this property of the system results from time oscillations that develop in the strategy distribution of the agents and that it can be described in terms of biased random walk theory.

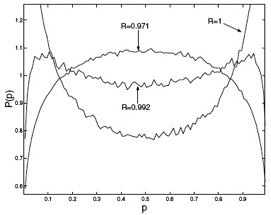

Agents strategy distribution as a function of the prize to fine ratio
(Hod & Nakar 2002)



